Вот и пролетела наша любимая Масленица с её ароматными блинами, весёлыми гуляньями и яркими традициями 😋

Теперь впереди целых семь недель Великого поста – время задуматься о духовных ценностях, укрепить здоровье и очистить душу от всего лишнего.

Что же делать дальше? А вот что:

✅ Отдохнуть после праздника и зарядиться энергией

✅ Составить план питания без мяса и рыбы (вегетарианские рецепты уже ждут вас!)

✅ Найти новые хобби или заняться спортом

✅ Больше времени проводить на свежем воздухе и наслаждаться природой 🌳

А вы как проводите первую неделю поста? Делитесь своими планами и впечатлениями в комментариях ниже ⬇️ Пусть этот период будет лёгким и светлым для каждого из нас!

Проводил отпуск в прошлом году в Светлогорске и вот таких милашей встретил.

Сейчас, в конце зимы, бутыль выглядит не очень хорошо (впрочем, как и во все прошлые зимы). Световой день для вербейника всё еще недостаточно длинный, и к концу февраля очень много побегов увяло. По опыту прошлых лет, бутыль должна проснуться в середине весны. Вот так выглядит бутыль сегодня снаружи и внутри:

Для сравнения, вот фотография с конца зимы прошлого года. Видно, что зелени в бутылке примерно столько же, сколько и сейчас. Ничего, за лето снова вырастет)

Теперь к результатам измерения концентрации CO2. Напомню, начиная с декабря, я измеряла концентрацию углекислого газа в бутылке двумя способами. Первый - с помощью жидкостного индикатора для аквариума. Второй - с помощью приборчика Даджет.

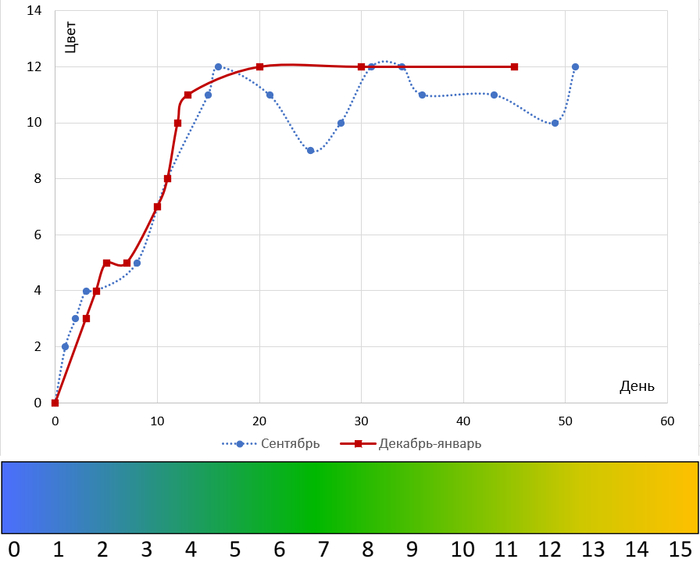
Начну с химического способа. Принцип действия жидкостного индикатора в аквариуме (цвет меняется в зависимости от рН, а рН зависит от растворенного СО2):

На этих графиках - результаты измерений жидкостным индикатором осенью и зимой

Предвидя возможный вопрос по поводу работоспособности жидкости два месяца спустя - да, она работает. После сентябрьских измерений я достала желто-зеленый пузырёк из банки и оставила его на подоконнике. Жидкость посинела обратно, значит, с ней все хорошо. На декабрьские измерения залила, конечно, свежую.

Думаю, что желто-зеленый цвет - это предел измерения данного индикатора, на самом деле концентрация углекислого газа может быть и выше. Осенью, когда зелени в бутылке было много, наблюдались эпизоды снижения от максимума. Сейчас, с коротким световым днём, снижений нет (по жидкостному индикатору).

Теперь про результаты измерений Даджетом. Датчик подключен к бутылке через длинную трубку, чтобы избежать попадания конденсата внутрь измерительного модуля. Если вода сконденсируется внутри датчика, то показания будут сильно искажаться. Впрочем, к Даджету у меня в любом случае есть много вопросов, я не особо доверяю его результатам.

В начале декабря ни разу не видела на табло Даджета значений выше 1500 ppm. В инструкции к прибору сказано, что он измеряет до 3000 ppm. Но на 12-ый день декабрьских измерений прибор резко ушёл за пределы измерительной шкалы (т.е. за 3000 ppm, если верить инструкции). Значений в интервале 1500-2999 я вообще не наблюдала, хотя цвет жидкости у индикатора менялся плавно.

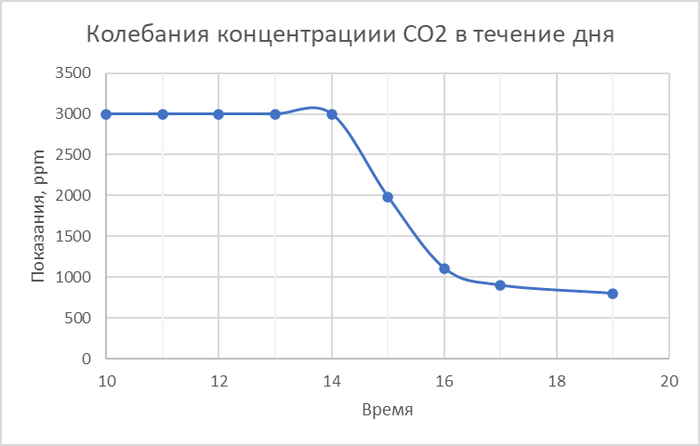
В январе Даджет "проснулся" и всё же стал показывать значения выше 1500 ppm. И вот какой график получился для почасовых измерений концентрации (усредненные значения):

В комментариях к моему прошлому посту #comment_377931059

#comment_377899078

совершенно правильно заметили, что в трубке и в бутыли концентрация углекислого газа может отличаться. Но еще раз, длинная трубка сделана для предотвращения конденсации жидкости. При высоком уровне влажности в бутылке ИК-датчик туда засовывать нельзя.

По итогам экспериментов вывод такой - простой ИК-датчик вроде Даджета и им подобных плохо подходит для измерений в такой системе. Жидкостной индикатор в условиях высокой влажности справляется лучше. Но им нельзя измерить колебания концентрации CO2 в течение дня (цвет жидкости меняется медленно). Попытка откалибровать цвет жидкости с помощью Даджета тоже оказалась неудачной - у ИК-датчика и у жидкостного слишком разное время реагирования на изменения концентрации.

На сегодня всё) Думаю, в следующий раз попробую провести серию измерений CO2 в разгаре лета, когда будет длинный световой день и много зелени в бутылке.

Кто хочет предыдущую серию про измерения почитать - мой прошлый пост Битва растений в бутылке: 2,5 года, комментарии к нему тоже интересные.

ТГ-канал https://t.me/mom_and_kids_creative